Find the values of k for which the roots are real and equal in each of the following equations:

Solution:

(i) The given quadric equation is $k x^{2}+4 x+1=0$, and roots are real and equal

Then find the value of $k$.

Here, $a=k, b=4$ and, $c=1$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k, b=4$ and, $c=1$

$=(4)^{2}-4 \times k \times 1$

$=16-4 k$

The given equation will have real and equal roots, if $D=0$

Thus,

$16-4 k=0$

$4 k=16$

$k=4$

Therefore, the value of $k=4$

(ii) The given quadric equation is $k x^{2}-2 \sqrt{5} x+4=0$, and roots are real and equal

Then find the value of k.

Here, $a=k, b=-2 \sqrt{5}$ and, $c=4$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k, b=-2 \sqrt{5}$ and, $c=4$

$=(2 \sqrt{5})^{2}-4 \times k \times 4$

$=20-16 k$

The given equation will have real and equal roots, if D = 0

Thus,

Therefore, the value of $k=\frac{5}{4}$

(iii) The given quadric equation is $3 x^{2}-5 x+2 k=0$, and roots are real and equal

Then find the value of k.

Here, $a=3, b=-5$ and, $c=2 k$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=3, b=-5$ and, $c=2 k$

$=(-5)^{2}-4 \times 3 \times k$

$=25-12 \mathrm{k}$

The given equation will have real and equal roots, if D = 0

 

Thus,

Therefore, the value of $k=\frac{25}{24}$

(iv) The given quadric equation is $4 x^{2}+k x+9=0$, and roots are real and equal Then find the value of $k$.

Here, $a=4, b=k$ and, $c=9$

As we know that $D=b^{2}-4 a c$

 

Putting the value of $a=4, b=k$ and, $c=9$

$=(k)^{2}-4 \times 4 \times 9$

 

$=k^{2}-144$

The given equation will have real and equal roots, if D = 0

Thus,

Therefore, the value of $k=\pm 12$

(v) The given quadric equation is $2 k x^{2}-40 x+25=0$, and roots are real and equal

Then find the value of k.

Here, $a=2 k, b=-40$ and, $c=25$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=2 k, b=-40$ and,$c=25$

$=(-40)^{2}-4 \times 2 k \times 25$

$=1600-200 k$

The given equation will have real and equal roots, if D = 0

Thus,

$1600-200 k=0$

$200 k=1600$

$k=\frac{1600}{200}$

$=8$

Therefore, the value of $k=8$

(vi) The given quadric equation is $9 x^{2}-24 x+k=0$, and roots are real and equal

Then find the value of k.

Here, $a=9, b=-24$ and,$c=k$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=9, b=-24$ and, $c=k$

$=(-24)^{2}-4 \times 9 \times k$

 

$=576-36 k$

The given equation will have real and equal roots, if D = 0

Thus,

Therefore, the value of $k=16$

(vii) The given quadric equation is $4 x^{2}-3 k x+1=0$, and roots are real and equal

Then find the value of $k$.

Here, $a=4, b=-3 k$ and,$c=1$

As we know that $D=b^{2}-4 a c$

 

Putting the value of $a=4, b=-3 k$ and, $c=1$

$=(-3 k)^{2}-4 \times 4 \times 1$

 

$=9 k^{2}-16$

The given equation will have real and equal roots, if D = 0

Thus,

$9 k^{2}-16=0$

$9 k^{2}=16$

$k=\sqrt{\frac{16}{9}}$

$=\pm \frac{4}{3}$

Therefore, the value of $k=\pm \frac{4}{3}$

(viii) The given quadric equation is $x^{2}-2(5+2 k) x+3(7+10 k)=0$, and roots are real and equal

Then find the value of k.

Here, $a=1, b=-2(5+2 k)$ and, $c=3(7+10 k)$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=1, b=-2(5+2 k)$ and, $c=3(7+10 k)$

$=(-2(5+2 k))^{2}-4 \times 1 \times 3(7+10 k)$

$=4\left(25+20 k+4 k^{2}\right)-12(7+10 k)$

$=100+80 k+16 k^{2}-84-120 k$

$=16-40 k+16 k^{2}$

The given equation will have real and equal roots, if D = 0

Thus,

$16-40 k+16 k^{2}=0$

$8\left(2 k^{2}-5 k+2\right)=0$

$\left(2 k^{2}-5 k+2\right)=0$

Now factorizing of the above equation

$\left(2 k^{2}-5 k+2\right)=0$

$2 k^{2}-4 k-k+2=0$

$2 k(k-2)-1(k-2)=0$

$(k-2)(2 k-1)=0$

So, either

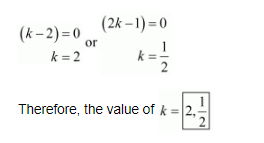
(ix) The given quadric equation is $(3 k+1) x^{2}+2(k+1) x+k=0$, and roots are real and equal

Then find the value of k.

Here, $a=(3 k+1), b=2(k+1)$ and,$c=k$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=(3 k+1), b=2(k+1)$ and, $c=k$

$=(2(k+1))^{2}-4 \times(3 k+1) \times k$

$=4\left(k^{2}+2 k+1\right)-4 k(3 k+1)$

$=4 k^{2}+8 k+4-12 k^{2}-4 k$

 

$=-8 k^{2}+4 k+4$

The given equation will have real and equal roots, if D = 0

Thus,

$-8 k^{2}+4 k+4=0$

$-4\left(2 k^{2}-k-1\right)=0$

$\left(2 k^{2}-k-1\right)=0$

Now factorizing of the above equation

 

$\left(2 k^{2}-k-1\right)=0$

$2 k^{2}-2 k+k-1=0$

$2 k(k-1)+1(k-1)=0$

$(k-1)(2 k+1)=0$

So, either

$(k-1)=0$

$k=1$

or

$(2 k+1)=0$

$k=\frac{-1}{2}$

Therefore, the value of $k=1, \frac{-1}{2} \mid$

(x) The given quadric equation is $k x^{2}+k x+1=-4 x^{2}-x$, and roots are real and equal

Then find the value of $k$.

 

Here,

$k x^{2}+k x+1=-4 x^{2}-x$

$4 x^{2}+k x^{2}+k x+x+1=0$

 

$(4+k) x^{2}+(k+1) x+1=0$

So,

$a=(4+k), b=(k+1)$ and, $c=1$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=(4+k), b=(k-1)$ and, $c=1$

$=(k+1)^{2}-4 \times(4+k) \times 1$

$=\left(k^{2}+2 k+1\right)-16-4 k$

 

$=k^{2}-2 k-15$

The given equation will have real and equal roots, if D = 0

Thus,

$k^{2}-2 k-15=0$

Now factorizing of the above equation

$k^{2}-2 k-15=0$

$k^{2}-5 k+3 k-15=0$

$k(k-5)+3(k-5)=0$

$(k-5)(k+3)=0$

So, either

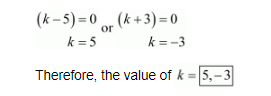
(xi) The given quadric equation is $(k+1) x^{2}+2(k+3) x+(k+8)=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=(k+1), b=2(k+3)$ and,$c=k+8$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=(k+1), b=2(k+3)$ and, $c=k+8$

$=(2(k+3))^{2}-4 \times(k+1) \times(k+8)$

$=\left(4 k^{2}+24 k+36\right)-4\left(k^{2}+9 k+8\right)$

$=4 k^{2}+24 k+36-4 k^{2}-36 k-32$

 

$=-12 k+4$

The given equation will have real and equal roots, if D = 0

$-12 k+4=0$

$k=\frac{4}{12}$

$=\frac{1}{3}$

Therefore, the value of $k=\frac{1}{3}$

(xii) The given quadric equation is $x^{2}-2 k x+7 k-12=0$, and roots are real and equal

Then find the value of k.

Here,

$a=1, b=-2 k$ and,$c=7 k-12$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=1, b=-2 k$ and, $c=7 k-12$

$=(-2 k)^{2}-4 \times 1 \times(7 k-12)$

 

$=4 k^{2}-28 k+48$

The given equation will have real and equal roots, if D = 0

$4 k^{2}-28 k+48=0$

 

$k^{2}-7 k+12=0$

Now factorizing of the above equation

$k^{2}-4 k-3 k+12=0$

$k(k-4)-3(k-4)=0$

 

$(k-4)(k-3)=0$

So, either

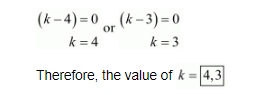
(xiii) The given quadric equation is $(k+1) x^{2}-2(3 k+1) x+8 k+1=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=k+1, b=-2(3 k+1)$ and, $c=8 k+1$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k+1, b=-2(3 k+1)$ and, $c=8 k+1$

$=(-2(3 k+1))^{2}-4 \times(k+1) \times(8 k+1)$

$=4\left(9 k^{2}+6 k+1\right)-4\left(8 k^{2}+9 k+1\right)$

$=36 k^{2}+24 k+4-32 k^{2}-36 k-4$

 

$=4 k^{2}-12 k$

The given equation will have real and equal roots, if D = 0

$4 k^{2}-12 k=0$

 

$k^{2}-3 k=0$

Now factorizing of the above equation

$k(k-3)=0$

So, either

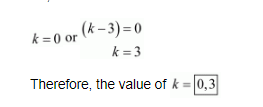
(xiv) The given quadric equation is $5 x^{2}-4 x+2+k\left(4 x^{2}-2 x-1\right)=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$5 x^{2}-4 x+2+k\left(4 x^{2}-2 x-1\right)=0$

$5 x^{2}-4 x+2+4 k x^{2}-2 k x-k=0$

 

$(5+4 k) x^{2}-(4+2 k) x+(2-k)=0$

So,

$a=(5+4 k), b=-(4+2 k)$ and, $c=(2-k)$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=(5+4 k), b=-(4+2 k)$ and,$c=(2-k)$

$=\{-(4+2 k)\}^{2}-4 \times(5+4 k) \times(2-k)$

$=\left(16+16 k+4 k^{2}\right)-4\left(10+3 k-4 k^{2}\right)$

$=16+16 k+4 k^{2}-40-12 k+16 k^{2}$

 

$=20 k^{2}+4 k-24$

The given equation will have real and equal roots, if D = 0

Thus,

$20 k^{2}+4 k-24=0$

$4\left(5 k^{2}+k-6\right)=0$

$\left(5 k^{2}+k-6\right)=0$

Now factorizing of the above equation

$\left(5 k^{2}+k-6\right)=0$

$5 k^{2}+6 k-5 k-6=0$

$k(5 k+6)-1(5 k+6)=0$

 

$(5 k+6)(k-1)=0$

So, either

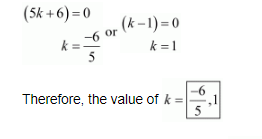
(xv) The given quadric equation is $(4-k) x^{2}+(2 k+4) x+8 k+1=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=4-k, b=(2 k+4)$ and,$c=8 k+1$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=4-k, b=(2 k+4)$ and, $c=8 k+1$

$=(2 k+4)^{2}-4 \times(4-k) \times(8 k+1)$

$=\left(4 k^{2}+16 k+16\right)-4\left(-8 k^{2}+31 k+4\right)$

$=4 k^{2}+16 k+16+32 k^{2}-124 k-16$

 

$=36 k^{2}-108 k+0$

The given equation will have real and equal roots, if D = 0

$36 k^{2}-108 k+0=0$

$36\left(k^{2}-3 k\right)=0$

 

$\left(k^{2}-3 k\right)=0$

Now factorizing of the above equation

$k(k-3)=0$

So, either

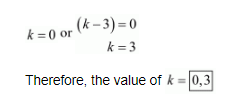
(xvi) The given quadric equation is $(2 k+1) x^{2}+2(k+3) x+k+5=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=(2 k+1), b=2(k+3)$ and,$c=k+5$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=(2 k+1), b=2(k+3)$ and, $c=k+5$

$=\{2(k+3)\}^{2}-4 \times(2 k+1) \times(k+5)$

$=\left\{4\left(k^{2}+6 k+9\right)\right\}-4\left(2 k^{2}+11 k+5\right)$

$=4 k^{2}+24 k+36-8 k^{2}-44 k-20$

 

$=-4 k^{2}-20 k+16$

The given equation will have real and equal roots, if D = 0

$-4 k^{2}-20 k+16=0$

$-4\left(k^{2}+5 k-4\right)=0$

 

$\left(k^{2}+5 k-4\right)=0$

Now factorizing the above equation

$\left(k^{2}+5 k-4\right)=0$

$k=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$k=\frac{-5 \pm \sqrt{25+16}}{2}$

$k=\frac{-5 \pm \sqrt{41}}{2}$

So, either

Therefore, the value of $k=\frac{-5 \pm \sqrt{41}}{2}$

(xvii) The given quadric equation is $4 x^{2}-2(k+1) x+k+4=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=4, b=-2(k+1)$ and,$c=k+4$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=4, b=-2(k+1)$ and, $c=k+4$

$=\{-2(k+1)\}^{2}-4 \times 4 \times(k+4)$

$=\left\{4\left(k^{2}+2 k+1\right)\right\}-16(k+4)$

$=4 k^{2}+8 k+4-16 k-64$

 

$=4 k^{2}-8 k-60$

The given equation will have real and equal roots, if D = 0

$4 k^{2}-8 k-60=0$

$4\left(k^{2}-2 k-15\right)=0$

 

$\left(k^{2}-2 k-15\right)=0$

Now factorizing of the above equation

$\left(k^{2}-2 k-15\right)=0$

$k^{2}+3 k-5 k-15=0$

$k(k+3)-5(k+3)=0$

 

$(k+3)(k-5)=0$

So, either

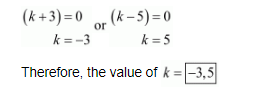
(xviii) The given quadric equation is $x^{2}-2(k+1) x+k^{2}=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=1, b=-2(k+1)$ and, $c=k^{2}$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=1, b=-2(k+1)$ and, $c=k^{2}$

$=\{-2(k+1)\}^{2}-4 \times 1 \times k^{2}$

$=\left\{4\left(k^{2}+2 k+1\right)\right\}-4 k^{2}$

$=4 k^{2}+8 k+4-4 k^{2}$

 

$=8 k+4$

The given equation will have real and equal roots, if D = 0

$8 k+4=0$

$8 k=-4$

$k=\frac{-4}{8}$

$=\frac{-1}{2}$

Therefore, the value of $k=\frac{-1}{2}$

(xix) The given quadric equation is $k^{2} x^{2}-2(2 k-1) x+4=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$a=k^{2}, b=-2(2 k-1)$ and,$c=4$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k^{2}, b=-2(2 k-1)$ and, $c=4$

$=\{-2(2 k-1)\}^{2}-4 \times k^{2} \times 4$

$=\left\{4\left(4 k^{2}-4 k+1\right)\right\}-16 k^{2}$

$=16 k^{2}-16 k+4-16 k^{2}$

 

$=-16 k+4$

The given equation will have real and equal roots, if D = 0

$-16 k+4=0$

 

$16 k=4$

$k=\frac{4}{16}$

$=\frac{1}{4}$

Therefore, the value of $k=\frac{1}{4}$

$(\mathrm{xx})$ The given quadric equation is $(k+1) x^{2}-2(k-1) x+1=0$, and roots are real and equal Then find the value of $k$.

 

Here,

$a=k+1, b=-2(k-1)$ and,$c=1$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k+1, b=-2(k-1)$ and, $c=1$

$=\{-2(k-1)\}^{2}-4 \times(k+1) \times 1$

$=\left\{4\left(k^{2}-2 k+1\right)\right\}-4 k-4$

$=4 k^{2}-8 k+4-4 k-4$

 

$=4 k^{2}-12 k+0$

The given equation will have real and equal roots, if D = 0

$4 k^{2}-12 k+0=0$

$4 k^{2}-12 k=0$

Now factorizing of the above equation

$4 k(k-3)=0$

 

$k(k-3)=0$

So, either

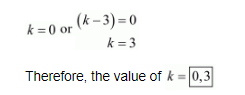
(xxi) The given quadric equation is $2 x^{2}+k x+3=0$, and roots are real and lequal

Then find the value of $k$.

 

Here,

$a=2, b=k$ and,$c=3$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=2, b=k$ and, $c=3$

$=k^{2}-4 \times 2 \times 3$

 

$=k^{2}-24$

The given equation will have real and equal roots, if D = 0

$k^{2}-24=0$

$k^{2}=24$

$k=\sqrt{24}$

$=\sqrt{4 \times 6}$

$-+2 \sqrt{6}$

Therefore, the value of $k=\pm 2 \sqrt{6}$

(xxii) The given quadric equation is $k x(x-2)+6=0$, and roots are real and equal

Then find the value of $k$.

 

Here,

$k x(x-2)+6=0$

 

$k x^{2}-2 k x+6=0$

So,

$a=k, b=-2 k$ and,$c=6$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k, b=-2 k$ and, $c=6$

$=(-2 k)^{2}-4 \times k \times 6$

 

$=4 k^{2}-24 k$

The given equation will have real and equal roots, if D = 0

$4 k^{2}-24 k=0$

Now factorizing of the above equation

$4 k(k-6)=0$

 

$k(k-6)=0$

So, either

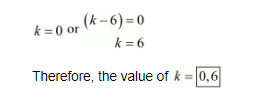
(xxiii) The given quadratic equation is $x^{2}-4 k x+k=0$, and roots are real and equal.

Then find the value of $k$.

 

Here,

$x^{2}-4 k x+k=0$

So,

$a=1, b=-4 k$ and $c=k$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=1, b=-4 k$ and $c=k$.

$D=(-4 k)^{2}-4(1)(k)$

$=16 k^{2}-4 k$

The given equation will have real and equal roots, if D = 0.

So, $16 k^{2}-4 k=0$

Now factorizing the above equation,

$16 k^{2}-4 k=0$

$\Rightarrow 4 k(4 k-1)=0$

$\Rightarrow 4 k=0$ or $4 k-1=0$

 

$\Rightarrow k=0$ or $k=\frac{1}{4}$

Therefore, the value of $k=0, \frac{1}{4}$.

(xxiv) The given quadratic equation is $k x(x-2 \sqrt{5})+10=0$, and roots are real and equal.

Then find the value of $k$.

 

Here,

$k x(x-2 \sqrt{5})+10=0$

$\Rightarrow k x^{2}-2 \sqrt{5} k x+10=0$

So,

$a=k, b=-2 \sqrt{5} k$ and $c=10$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=k, b=-2 \sqrt{5} k$ and $c=10$.

$D=(-2 \sqrt{5} k)^{2}-4(k)(10)$

$=20 k^{2}-40 k$

The given equation will have real and equal roots, if D = 0.

So, $20 k^{2}-40 k=0$

Now factorizing the above equation,

$20 k^{2}-40 k=0$

$\Rightarrow 20 k(k-2)=0$

$\Rightarrow 20 k=0$ or $k-2=0$

 

$\Rightarrow k=0$ or $k=2$

Therefore, the value of $k=0,2$.

(xxv) The given quadratic equation is $p x(x-3)+9=0$, and roots are real and equal.

Then find the value of $p$.

 

Here,

$p x(x-3)+9=0$

$\Rightarrow p x^{2}-3 p x+9=0$

So,

$a=p, b=-3 p$ and $c=9$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=p, b=-3 p$ and $c=9$.

$D=(-3 p)^{2}-4(p)(9)$

$=9 p^{2}-36 p$

The given equation will have real and equal roots, if D = 0.

So, $9 p^{2}-36 p=0$

Now factorizing the above equation,

$9 p^{2}-36 p=0$

$\Rightarrow 9 p(p-4)=0$

$\Rightarrow 9 p=0$ or $p-4=0$

 

$\Rightarrow p=0$ or $p=4$

Therefore, the value of p=0, 4.">p=0, 4

( $\mathrm{xxvi)}$ The given quadratic equation is $4 x^{2}+p x+3=0$, and roots are real and equal.

Then find the value of $p$.

p=0, 4.">Here,

p=0, 4.">$4 x^{2}+p x+3=0$

p=0, 4.">So,

p=0, 4.">$a=4,b=p$and$c=3$

p=0, 4.">As we know that$D=b^{2}-4 a c$

p=0, 4.">Putting the value of $a=4, b=p$ and $c=3$.

p=0, 4.">$D= (p)^{2}-4(4)(3)$

The given equation will have real and equal roots, if D = 0.

So, $p^{2}-48=0$

Now factorizing the above equation,

$p^{2}-48=0$

$\Rightarrow p^{2}-(4 \sqrt{3})^{2}=0$

 

$\Rightarrow(p-4 \sqrt{3})(p+4 \sqrt{3})=0$

$\Rightarrow p-4 \sqrt{3}=0$ or $p+4 \sqrt{3}=0$

 

$\Rightarrow p=4 \sqrt{3}$ or $p=-4 \sqrt{3}$

Therefore, the value of $p=\pm 4 \sqrt{3}$.

 

 

 

 

 

20k2-40k=0⇒20kk-2=0⇒20k=0 or k-2=0⇒k=0 or k=2">