Question:
Find the weight of a hollow sphere of metal having internal and external diameters as $20 \mathrm{~cm}$ and $22 \mathrm{~cm}$, respectively if $1 \mathrm{~m}^{3}$ of metal weighs $21 \mathrm{~g}$.
Solution:
External radius of hollow sphere, $r_{1}=\frac{22}{2}=11 \mathrm{~cm}$
Internal radius of hollow sphere, $r_{2}=\frac{20}{2}=10 \mathrm{~cm}$
The volume of hollow sphere $=\frac{4}{3} \pi\left(r_{1}^{3}-r_{2}^{2}\right)$
$=\frac{4}{3} \pi\left(11^{3}-10^{3}\right)$
$=\frac{4}{3} \pi \times 331$
$=\frac{1324 \times 22}{21}$
The volume of hollow sphere $=\frac{1324 \times 22}{21}$
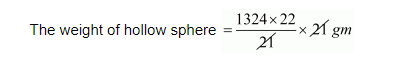
$=29128 \mathrm{gm}$
$=29.13 \mathrm{~kg}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.