Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Fig. 1.12).
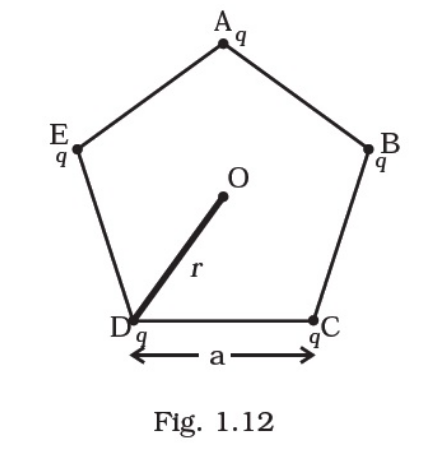
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
(a) (i) Here, point $O$ is equidistant from all the charges at the end point of peatagon. Thus. due to symmetry, the forces due to all the charges are cancelled out: As a result electric field at $O$ is zero.
(ii) When charge $q$ is removed, it is equivalent to placing a $-q$ charge at the same point. The electric field at point $\mathrm{O}$ would be
$\vec{E}=\frac{q}{4 \pi s_{0} r^{2}}$ along $\overrightarrow{O A}$
(iii) If charge $q$ at $A$ is replaced by $-q$, which is equivalent to placing two negative charges i. e., $2 q$ at the same point. So value of electric field would be
$\overrightarrow{E^{\prime}}=\frac{2 q}{4 \pi s_{o} r^{2}}$ along $\overrightarrow{O A}$
(b) If pentagon shown here is replaced by any n sided regular polygon with charge q at each of its corners, the electric filed at $O$ would continue to be zero.
