Question:
For any sets A and B, prove that:
(i) $A \cap B^{\prime}=\phi \Rightarrow A \subset B$
(ii) $A^{\prime} \cup B^{\prime}=U \Rightarrow A \subset B$
Solution:
(i) The Venn Diagram for the given condition is given below
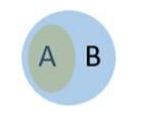
As can be seen from the Venn Diagram, A is a proper subset of B
$\Rightarrow \mathrm{A} \subset \mathrm{B}$
(ii) Wrong question. If $A$ is a proper subset of $B$ then $A^{, U} B^{\prime} \neq U$
