For following reactions:
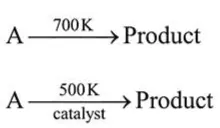
it was found that the $E_{a}$ is decrease by $30 \mathrm{~kJ} / \mathrm{mol}$ in the presence of catalyst. If the rate remains unchanged, the activation energy for catalysed reaction is (Assume pre exponential factor is same):
Correct Option: 1
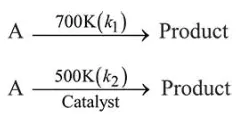
Given: $k_{1}=k_{2}$
$\mathrm{Ae}^{-\frac{\mathrm{E}_{a_{1}}}{\mathrm{RT}_{1}}}=\mathrm{Ae}^{-\frac{\mathrm{E}_{a_{2}}}{\mathrm{RT}_{2}}}$
$\frac{\mathrm{E}_{a_{1}}}{\mathrm{~T}_{1}}=\frac{\mathrm{E}_{a_{2}}}{\mathrm{~T}_{2}}$
$\mathrm{E}_{a_{2}}=\mathrm{E}_{a_{1}}-30$
$\Rightarrow \mathrm{E}_{a 1}=\mathrm{E}_{a_{2}}+30$
$\frac{\mathrm{E}_{a_{2}}+30}{\mathrm{~T}_{1}}=\frac{\mathrm{E}_{a_{2}}}{\mathrm{~T}_{2}}$
$\frac{\mathrm{E}_{a_{2}}+30}{700}=\frac{\mathrm{E}_{a_{2}}}{500}$
$\Rightarrow 150=2 \mathrm{E}_{a_{2}}$
$\mathrm{E}_{a_{2}}=75 \mathrm{~kJ} / \mathrm{mol}$
