For the given cell ;
$\mathrm{Cu}(\mathrm{s})\left|\mathrm{Cu}^{2+}\left(\mathrm{C}_{1} \mathrm{M}\right) \| \mathrm{Cu}^{2+}\left(\mathrm{C}_{2} \mathrm{M}\right)\right| \mathrm{Cu}(\mathrm{s})$ change in Gibbs energy $(\Delta \mathrm{G})$ is negative, if :
Correct Option: , 4
$\Delta \mathrm{G}=-\mathrm{n} \mathrm{F} \mathrm{E}_{\mathrm{cell}}$
Anode : $\quad \mathrm{Cu}(\mathrm{s}) \longrightarrow \mathrm{Cu}^{+2}\left(\mathrm{C}_{1}\right)+2 \mathrm{e}^{-}: \mathrm{E}^{\circ}$
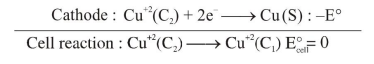
$E_{\text {cell }}=E_{\text {cell }}^{\circ}-\frac{2.303 R T}{n F} \log Q$
$\mathrm{E}_{\text {cell }}=0-\frac{2.303 \mathrm{RT}}{\mathrm{nF}} \log \left(\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\right)$
$\mathrm{E}_{\text {cell }}>0:$ if $\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}<1 \Rightarrow \mathrm{C}_{1}<\mathrm{C}_{2}$
