For which values of a and b,

Given that the zeroes of q(x) = x3 + 2x2 + a are also the zeroes of the polynomial p(x) = x5 – x4 – 4x3 + 3xz + 3x + b i.e., q(x) is a factor of p(x). Then, we use a division algorithm.

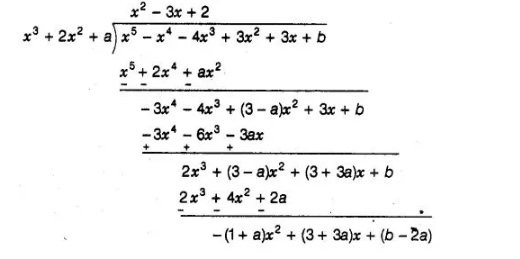
If (x3 + 2x2 + a) is a factor of (x5 – x4 – 4x3 + 3x2 + 3x + b), then remainder should be zero.

i.e.,        – (1 + a) x2 + (3 + 3a) x + (b – 2a) = 0

= 0.x2 + 0.x+0

On comparing the coefficient of x, we get

a + 1 = 0

⇒a = -1

and b – 2a = 0

⇒b =2a

b = 2(-1) = -2                                                   [va = -1]

For a = -1 and b = – 2, the zeroes ofq(x) are also the zeroes of the polynomial p(x).

∴                                              q(x) = x3 + 2x2 -1

and                                           p(x) = x5 – x4 – 4x3 + 3x2 + 3x – 2

Now,                  Divident = divisor xquotient + remainder

p(x) = (x3 +2x2 -1)(x2 -3x + 2)+ 0

= (x3 + 2x2 -1){x2 -2x – x + 2}

= (x3 + 2x2 – 1) (x – 2) (x – 1)

Hence, the zeroes of p(x) are land 2 which are not the zeroes of q(x).