Four equal circles, each of radius a, touch each other.

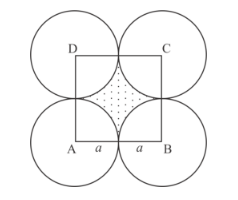
It is given that four equal circles of radius a touches each other.

So, Area of circle $=\pi a^{2}$

Since circles touches each other, the lines joining their centre make a square ABCD.

The side of square is 2a.

Area of quadrant inside square $=\frac{1}{4} \pi a^{2}$

Area of shaded region $=$ Area of square $-4 \times$ Area of quadrant

$=(2 a)^{2}-4 \times \frac{\pi a^{2}}{4}$

$=4 a^{2}-\frac{22}{7} a^{2}$

$=\frac{6}{7} a^{2}$