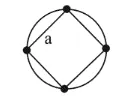
Four identical particles of mass $\mathrm{M}$ are located at the corners of a square of side ' $a$ '. What should be their speed if each of them revolves under the influence of others' gravitational field in a circular orbit circumscribing the square ?
Correct Option: , 2
(2) $A C=a \sqrt{2} \quad \because r=\frac{A C}{2}=\frac{a \sqrt{2}}{2}=\frac{a}{\sqrt{2}}$
Resultant force on the body
$B=\frac{G M^{2}}{a^{2}} \hat{i}+\frac{G M^{2}}{a^{2}} \hat{j}+\frac{G M^{2}}{(a \sqrt{2})^{2}}$
$\left(\cos 45^{\circ} \hat{i}+\sin 45^{\circ} \hat{j}\right)$
$\Rightarrow|F|=\frac{G M^{2}}{a^{2}}(\sqrt{2})+\frac{G M^{2}}{2 a^{2}}$
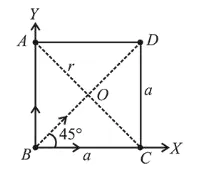
$\frac{M v^{2}}{r}=$ Resultant force towards centre
$\therefore \frac{M v^{2}}{\left(\frac{a}{\sqrt{2}}\right)}=\frac{G M^{2}}{a^{2}}\left(\sqrt{2}+\frac{1}{2}\right)$
$\Rightarrow v^{2}=\frac{G M}{a}\left(1+\frac{1}{2 \sqrt{2}}\right)$
$\Rightarrow v=\sqrt{\frac{G M}{a}\left(1+\frac{1}{2 \sqrt{2}}\right)}=1.16 \sqrt{\frac{G M}{a}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.