Question:
Four point masses, each of mass $m$, are fixed at the corners of a square of side $l$. The square is rotating with angular frequency $\omega$, about an axis passing through one of the corners of the square and parallel to its diagonal, as shown in the figure. The angular momentum of the square about this axis is:
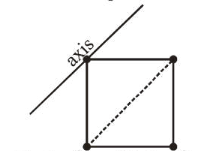
Correct Option: , 3
Solution:
(3) Angular momentum, $L=I \omega$
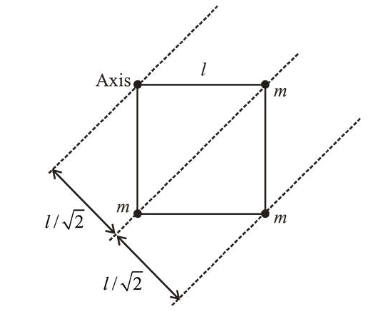
$I=m(0)^{2}+m\left(\frac{l}{\sqrt{2}}\right)^{2} \times 2+m(\sqrt{2} l)^{2}$
$=\frac{2 m l^{2}}{2}+2 m l^{2}=3 m l^{2}$
Angular momentum $L=I \omega=3 \mathrm{ml}^{2} \omega$
