Four resistances of $15 \Omega, 12 \Omega^{2}, 4 \Omega$ and $10 \Omega$ respectively in cyclic order to form Wheatstone's network. The resistance that is to be connected in parallel with the resistance of $10 \Omega$ to balance the network is_____$\Omega$
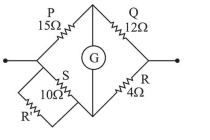
As per Wheatstone bridge balance condition $\frac{P}{Q}=\frac{S}{R}$
Let resistance $R^{\prime}$ is connected in parallel with resistance S of $10 \Omega$
$\therefore \frac{15}{12}=\frac{10 R^{\prime}}{\frac{10+R^{\prime}}{4}} \Rightarrow 5=\frac{10 R^{\prime}}{10+R^{\prime}}$
$\Rightarrow 50+5 R^{\prime}=10 R^{\prime}$
$\therefore R^{\prime}=\frac{50}{5}=10 \Omega$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
