From a point on the ground,

It is given that tower is placed at a 20 m high building. The top and bottom of the tower makes an angle of   respectively with the ground.

We have to find the height of the tower.

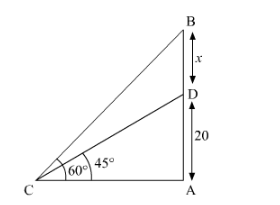
Let DB is the tower

Let AD is the building

Height of the building = 20 m

Height of the tower = x m

According to the figure,

$\frac{A B}{A C}=\tan 60^{\circ}$

$A C=\frac{A B}{\tan 60^{\circ}}$.......(1)

$\frac{A D}{A C}=\tan 45^{\circ}$

$A C=\frac{A D}{\tan 45^{\circ}} \ldots \ldots(2)$

Since (1) = (2)

$\frac{A B}{\tan 60^{\circ}}=\frac{A D}{\tan 45^{\circ}}$

$\frac{20+x}{\sqrt{3}}=\frac{20}{1}$

$20+x=20 \sqrt{3}$

$x=20 \sqrt{3}-20$

$x=20(\sqrt{3}-1)$

$x=20 \times 0.732$

$x=14.64 \mathrm{~m}$