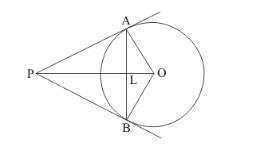
From a point P, two tangents PA and PB are drawn to a circle with centre O.

Let us first put the given data in the form of a diagram.

Consider and. We have,

PO is the common side for both the triangles.

PA = PB(Tangents drawn from an external point will be equal in length)

OB = OA(Radii of the same circle)

Therefore, by SSS postulate of congruency, we have

$\triangle \mathrm{POA} \cong \triangle \mathrm{POB}$

Hence,

$\angle O P A=\angle O P B$............(1)

Now let us consider $\triangle P L A$ and $\triangle P L B$. We have,

PL is the common side for both the triangles.

 (From equation (1))

PA = PB (Tangents drawn from an external point will be equal in length)

From SAS postulate of congruent triangles,

Therefore,

PL = LB …… (2)

$\angle P L A=\angle P L B$

Since AB is a straight line,

$\angle A L B=180^{\circ}$

$\angle P L A+\angle P L B=180^{\circ}$

$2 \angle P L A=180^{\circ}$

$\angle P L A=90^{\circ}$

$\angle P L B=90^{\circ}$

Let us now take up ΔOPB. We know that the radius of a circle will always be perpendicular to the tangent at the point of contact. Therefore,

$\angle O B P=90^{\circ}$

By Pythagoras theorem we have,

$P B^{2}=O P^{2}-O B^{2}$

By Pythagoras theorem we have,

$P B^{2}=O P^{2}-O B^{2}$

It is given that

OP = diameter of the circle

Therefore,

OP = 2OB

Hence,

$P B^{2}=(2 O B)^{2}-O B^{2}$

$P B^{2}=4 O B^{2}-O B^{2}$

$P B^{2}=3 O B^{2}$

$P B=\sqrt{3} O B$

Consider $\triangle P L B$. We have,

$L B^{2}=P B^{2}-P L^{2}$

But we have found that,

$P B=\sqrt{3} O B$

Also from the figure, we can sayPL = PO − OL 

Therefore,

$L B^{2}=3 O B^{2}-[P O-O L]^{2} \ldots \ldots(3)$

Also, from , we have

$L B^{2}=O B^{2}-O L^{2}$

Since Left Hand Sides of equation (3) and equation (4) are same, we can equate the Right Hand Sides of the two equations. Thus we have,

$O B^{2}-O L^{2}=3 O B^{2}-[P O-O L]^{2}$

$O B^{2}-O L^{2}=3 O B^{2}-\left[P O^{2}+O L^{2}-2 . P O . O L\right]$

$O B^{2}-O L^{2}=3 O B^{2}-P O^{2}-O L^{2}+2 . P O . O L$

We know from the given data, that OP = 2.OB. Let us substitute 2OB in place of PO in the above equation. We get,

$O B^{2}-O L^{2}=3 O B^{2}-(2 O B)^{2}-O L^{2}+2.2 . O B . O L$

$O B^{2}-O L^{2}=3 O B^{2}-4 O B^{2}-O L^{2}+4 . O B . O L$

$2 O B^{2}=4 . O B . O L$

$O L=\frac{O B}{2}$

Substituting the value of OL and also PO in equation (3), we get,

$L B^{2}=3 O B^{2}-\left[2 O B-\left(\frac{O B}{2}\right)\right]^{2}$

$L B^{2}=3 O B^{2}-\left[4 O B^{2}+\left(\frac{O B^{2}}{4}\right)-2 . O B^{2}\right]$

$L B^{2}=3 O B^{2}-4 O B^{2}-\left(\frac{O B^{2}}{4}\right)+2 . O B^{2}$

$L B^{2}=\frac{3 O B^{2}}{4}$

$L B=\frac{\sqrt{3} O B}{2}$

Also from the figure we get,

AB = PL + LB

From equation (2), we know that PL = LB. Therefore,

AB = 2.LB

$A B=2 \times \frac{\sqrt{3} O B}{2}$

$A B=\sqrt{3} O B$

We have also found that. We know that tangents drawn from an external point will be equal in length. Therefore, we have

PA = PB

Hence,

PA = 

Now, consider . We have,

PA = 

PB = 

AB = 

Since all the sides of the triangle are of equal length, is an equilateral triangle. Thus we have proved.