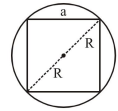
Question: From a solid sphere of mass $\mathrm{M}$ and radius $\mathrm{R}$ a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is:-
$\frac{4 \mathrm{MR}^{2}}{9 \sqrt{3} \pi}$
$\frac{4 \mathrm{MR}^{2}}{3 \sqrt{3} \pi}$
$\frac{\mathrm{MR}^{2}}{32 \sqrt{2} \pi}$
$\frac{\mathrm{MR}^{2}}{16 \sqrt{2} \pi}$
Correct Option: 1
Solution: