From an external point P, tangents PA and PB are drawn to a circle with centre O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of Δ PCD.
Let us first put the given data in the form of a diagram.
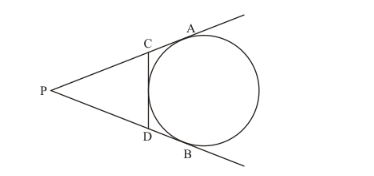
It is given that PA = 14cm. we have to find the perimeter of
.
Perimeter of is PC + CD + PD
Looking at the figure we can rewrite the equation as follows.
Perimeter of is PC + CE + ED + PD ……(1)
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
CE =CA
ED =DB
Replacing the above in equation (1), we have,
Perimeter of as PC + CA + DB + PD
By looking at the figure we get,
PC +CA =PA
DB +PD =PB
Therefore,
Perimeter of is PA + PB
It is given that PA = 14 cm. again from the same property of tangents which says that the length of two tangents drawn to a circle from the same external point will be equal, we have,
PA = PB
Therefore,
Perimeter of = 2PA
Perimeter of = 2 × 14
Perimeter of = 28
Thus perimeter of is 28 cm.