From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
$\frac{h(\tan \alpha+\tan \beta)}{\tan \alpha+\tan \beta}$ metres.
Let 
be the height of light house
. And an angle of depression of the top of light house from two ships are 
and
respectively. Let
, 
. And 
, 
.
We have to find distance between the ships
We have the corresponding figure as follows
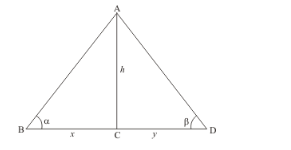
We use trigonometric ratios.
In $\triangle A B C$
$\Rightarrow \quad \tan \alpha=\frac{A C}{B C}$
$\Rightarrow \quad \tan \alpha=\frac{h}{x}$
$\Rightarrow \quad x=\frac{h}{\tan \alpha}$
Again in $\triangle A D C$
$\Rightarrow \quad \tan \beta=\frac{A C}{C D}$
$\Rightarrow \quad \tan \beta=\frac{h}{y}$
$\Rightarrow \quad y=\frac{h}{\tan \beta}$
Now,
$\Rightarrow \quad B D=x+y$
$\Rightarrow \quad B D=\frac{h}{\tan \alpha}+\frac{h}{\tan \beta}$
$\Rightarrow \quad B D=\frac{h(\tan \alpha+\tan \beta)}{\tan \alpha \tan \beta}$Hence the distance between ships is $\frac{h(\tan \alpha+\tan \beta)}{\tan \alpha \tan \beta}$