Give an example of a function which is

(i) one - one but not onto

$f(x)=6 x$

For One - One

$f\left(x_{1}\right)=6 x_{1}$

$f\left(x_{2}\right)=6 x_{2}$

put $f\left(x_{1}\right)=f\left(x_{2}\right)$ we get

$6 x_{1}=6 x_{2}$

Hence, if $f\left(x_{1}\right)=f\left(x_{2}\right), x_{1}=x_{2}$

Function $f$ is one - one

For Onto

$f(x)=6 x$

let $f(x)=y$, such that $y \in N$

$6 x=y$

$\Rightarrow x=\frac{y}{6}$

If $y=1$

$x=\frac{1}{6}=0.166667$

which is not possible as $x \in N$

Hence, $f$ is not onto.

(ii) one - one and onto

$f(x)=x^{5}$

$\Rightarrow y=x^{5}$

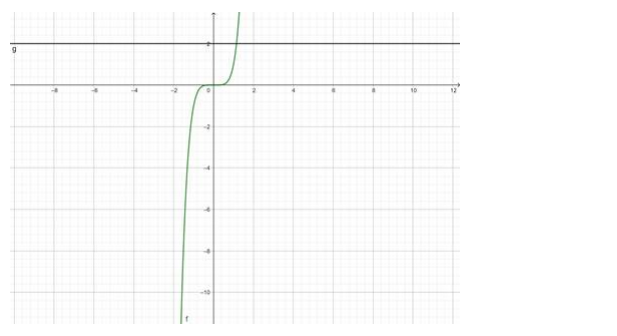
Since the lines do not cut the curve in 2 equal valued points of $y$, therefore, the function $f(x)$ is one - one.

The range of $f(x)=(-\infty, \infty)=R$ (Codomain)

$\therefore f(x)$ is onto

$\therefore f(x)$ is one - one and onto.

(iii) neither one - one nor onto

$f(x)=x^{2}$

for one one:

$f\left(x_{1}\right)=\left(x_{1}\right)^{2}$

$f\left(x_{2}\right)=\left(x_{2}\right)^{2}$

$f\left(x_{1}\right)=f\left(x_{2}\right)$

$\Rightarrow\left(x_{1}\right)^{2}=\left(x_{2}\right)^{2}$

$\Rightarrow x_{1}=x_{2}$ or $x_{1}=-x_{2}$

Since $x_{1}$ does not have a unique image it is not one - one

For onto

$f(x)=y$

such that $y \in R$

$x^{2}=y$

$\Rightarrow x=\pm \sqrt{y}$

If $y$ is negative under root of a negative number is not real

Hence, $f(x)$ is not onto.

$\therefore f(x)$ is neither onto nor one - one

(iv) onto but not one - one.

Consider a function $f: Z \rightarrow N$ such that $f(x)=|x| .$

Since the Z maps to every single element in N twice, this function is onto but not one - one.

$Z$ - integers

N - natural numbers.