Given below are two statements :
Statement I : An electric dipole is placed at the centre of a hollow sphere. The flux of electric field through the sphere is zero but the electric field is not zero anywhere in the sphere.
Statement II : If $R$ is the radius of a solid metallic sphere and $\mathrm{Q}$ be the total charge on it. The electric field at any point on the spherical surface of radius $r(
Correct Option: , 2
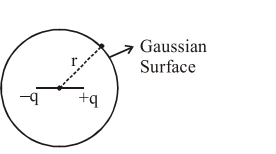
$\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}_{\mathrm{in}}}{\varepsilon_{0}}=0=\phi$
Flux of $\overrightarrow{\mathrm{E}}$ through sphere is zero.
But $\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=0 \Rightarrow\{\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}} \neq 0\}$ for small section $\mathrm{ds}$
only
Statement-2
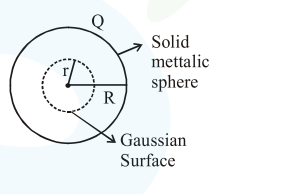
As change encloses within gaussian surface is equal to zero.
$\phi=\oint \overrightarrow{\mathrm{E}} \cdot \overline{\mathrm{ds}}=0$
Option(2) statement- 1 correct statement- 2 false.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
