Given: $f(x)=\left\{\begin{array}{cc}x & , 0 \leq x<\frac{1}{2} \\ \frac{1}{2} & , \quad x=\frac{1}{2} \\ 1-x & , \quad \frac{1}{2} and $g(x)=\left(x-\frac{1}{2}\right)^{2}, x \in \mathrm{R}$. Then the area (in sq. units) of the region bounded by the curves, $y=f(x)$ and $y=g(x)$ between the lines, $2 x=1$ and $2 x=\sqrt{3}$, is :
Correct Option: , 2
Coordinates of $P\left(\frac{1}{2}, 0\right), Q\left(\frac{\sqrt{3}}{2}, 0\right), R\left(\frac{\sqrt{3}}{2}, 1-\frac{\sqrt{3}}{2}\right)$
and $S\left(\frac{1}{2}, \frac{1}{2}\right)$
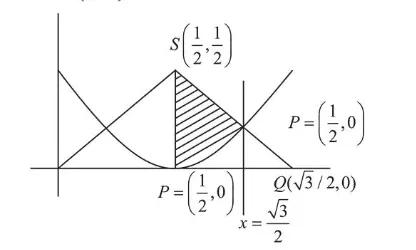
Required area = Area of trapezium $P Q R S$
$-\int_{1 / 2}^{\sqrt{3} / 2}\left(x-\frac{1}{2}\right)^{2} d x$
$=\frac{1}{2}\left(\frac{\sqrt{3}-1}{2}\right)\left(\frac{1}{2}+1-\frac{\sqrt{3}}{2}\right)-\frac{1}{3}\left(\left(x-\frac{1}{2}\right)^{3}\right)_{1 / 2}^{\sqrt{3} / 2}$
$=\frac{\sqrt{3}}{4}-\frac{1}{3}$
