Question:
Given the following two statements :
$\left(S_{1}\right):(q \vee p) \rightarrow(p \leftrightarrow \sim q)$ is a tautology.
$\left(S_{2}\right): \sim q \wedge(\sim p \leftrightarrow q)$ is a fallacy. Then :
Correct Option: , 4
Solution:
The truth table of both the statements is
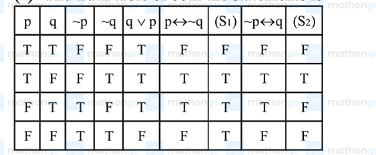
$\therefore \mathrm{S}_{1}$ is not tautology and
$\mathrm{S}_{2}$ is not fallacy.
Hence, both the statements $\left(S_{1}\right)$ and $\left(S_{2}\right)$ are not correct.
