If a square is inscribed in a circle,

Let ABCD be the square inscribed in a circle of radius r.

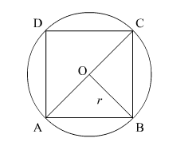
Here, OA = OB = r.

$\therefore O A^{2}+O B^{2}=A B^{2}$

$\Rightarrow r^{2}+r^{2}=\mathrm{AB}^{2}$

$\Rightarrow 2 r^{2}=\mathrm{AB}^{2}$

Now, area of square $\mathrm{ABCD}=\mathrm{AB}^{2}=2 r^{2}$

Area of circle $=\pi r^{2}$

Now we will find the ratio of area of the circle and the square.

$\frac{\text { Area of circle }}{\text { Area of square }}=\frac{\pi r^{2}}{2 r^{2}}=\frac{\pi}{2}$

Hence, the ratio of area of the circle and square is $\pi: 2$.