If AB, AC, PQ are tangents in the given figure and AB = 5 cm,

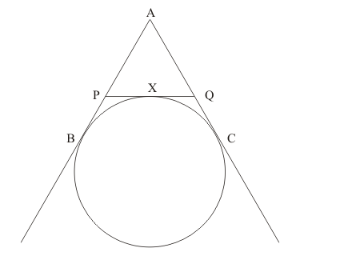
We have been asked to find the perimeter of the triangle APQ.

Therefore,

Perimeter of ΔAPQ is equal to AP + AQ + PQ

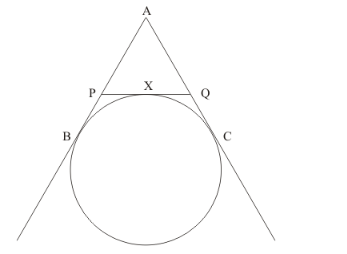
By looking at the figure, we can rewrite the above as follows,

Let the Perimeter of ΔAPQ be P. So P= AP + AQ + PX + XQ

From the property of tangents we know that when two tangents are drawn to a circle from the same external point, the length of the two tangents will be equal. Therefore we have,

PX =PB

XQ =QC

Replacing these in the above equation we have,

P =AP + AQ + PB + QC

From the figure we can see that,

AP + PB = AB

AQ + QC = AC

Therefore, we have, P= AB + AC

It is given that AB = 5 cm.

Again from the same property of tangents we know that that when two tangents are drawn to a circle from the same external point, the length of the two tangents will be equal. Therefore we have,

AB = AC

Therefore,

AC = 5 cm

Hence,

P = 5 + 5=10

Thus the perimeter of triangle APQ is 10 cm.