If non-parallel sides of a trapezium are equal,

Given ABCD is a trapezium whose non-parallel sides AD and BC are equal.

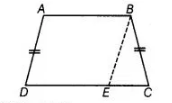
To prove Trapezium $A B C D$ is a cyclic:

Join $B E$, where $B E \| A D$.

Proof Since, $A B \| D E$ and $A D \| B E$

Since, the quadrilateral $A B E D$ is a parallelogram.

$\therefore$ $\angle B A D=\angle B E D$ $\ldots($ (i)

[opposite angles of a paralleiogram are equal]

and  $A D=B E$   

[opposite sides of a parallelogram are equal]

But $A D=B C$ [given] ... (iii)

From Eqs. (ii) and (iii),  $B C=B E$

$\Rightarrow$ $\angle B E C=\angle B C E$ ...(iv)

[angles opposite to equal sides are equal]

Also, $\angle B E C+\angle B E D=180^{\circ}$ [linear pair axiom]

$\therefore$ $\angle B C E+\angle B A D=180^{\circ}$ [from Eqs. (i) and (iv)]

If sum of opposite angles of a quadrilateral is $180^{\circ}$, then quadrilateral is cyclic.

Hence, trapezium $A B C D$ is a cyclic. 

Hence proved.