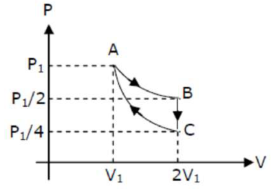
If one mole of an ideal gas at $\left(P_{1}, V_{1}\right)$ is allowed to expand reversibly and isothemally $(A$ to B) its pressure is reduced to one-half of the original pressure (see figure). This is followed by a constant volume cooling till its pressure is reduced to one-fourth of the initial value $(\mathrm{B} \rightarrow \mathrm{C})$. Then it is restored to its initial state by a reversible adiabutic compression ( $C$ to A). The net workdone by the gas is equal to :
Correct Option: , 3
(3)
$\mathrm{AB} \rightarrow$ Isothermal process $\mathrm{W}_{\mathrm{AB}} \rightarrow \mathrm{nRT} \ln 2=\mathrm{RT} \ln 2$
$\mathrm{BC} \rightarrow$ Isochoric process $\mathrm{W}_{\mathrm{BC}}=0$
$\mathrm{CA} \rightarrow$ Adiabatic process $W_{C A}=\frac{P_{1} V_{1}-\frac{P_{1}}{4} \times 2 V_{1}}{1-\gamma}=\frac{P_{1} V_{1}}{2(1-\gamma)}=\frac{R T}{2(1-\gamma)}$
$\mathrm{W}_{\mathrm{ABCA}}=\mathrm{RT} / \mathrm{n} 2+\frac{\mathrm{RT}}{2(1-\gamma)}$
$\left.=\mathrm{RT} \mid \ln 2-\frac{1}{2(\gamma-1)}\right\rceil$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.