If one of the angles of a triangle is 130° then the angle between the bisectors of the other two angles can be

Let ∆ABC be such that ∠A = 130°.

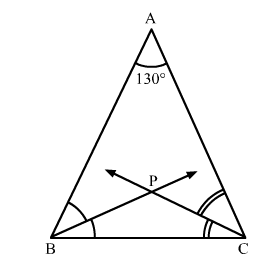
Here, BP is the bisector of ∠B and CP is the bisector of ∠C.

$\therefore \angle \mathrm{ABP}=\angle \mathrm{PBC}=\frac{1}{2} \angle \mathrm{B}$ .......(1)

Also, $\angle \mathrm{ACP}=\angle \mathrm{PCB}=\frac{1}{2} \angle \mathrm{C}$ ............(2)

In ∆ABC,

∠A + ∠B + ∠C = 180°         (Angle sum property)

⇒ 130° + ∠B + ∠C = 180°

⇒ ∠B + ∠C = 180° − 130° = 50°

$\Rightarrow \frac{1}{2} \angle B+\frac{1}{2} \angle C=\frac{1}{2} \times 50^{\circ}=25^{\circ}$

⇒ ∠PBC + ∠PCB = 25°     .....(3)     [Using (1) and (2)]

In ∆PBC,

∠PBC + ∠PCB + ∠BPC = 180°         (Angle sum property)

⇒ 25° + ∠BPC = 180°                       [Using (3)]

⇒ ∠BPC = 180° − 25° = 155°

Thus, if one of the angles of a triangle is 130° then the angle between the bisectors of the other two angles is 155°.

Hence, the correct answer is option (d).