If P and Q are two statements,

Question:

If $P$ and $Q$ are two statements, then which of the following compound statement is a tautology?

  1. (1) $((\mathrm{P} \Rightarrow \mathrm{Q}) \wedge \sim \mathrm{Q}) \Rightarrow \mathrm{Q}$

  2. (2) $((\mathrm{P} \Rightarrow \mathrm{Q}) \wedge \sim \mathrm{Q}) \Rightarrow \sim \mathrm{P}$

  3. (3) $((\mathrm{P} \Rightarrow \mathrm{Q}) \wedge \sim \mathrm{Q}) \Rightarrow \mathrm{P}$

  4. (4) $((\mathrm{P} \Rightarrow \mathrm{Q}) \wedge \sim \mathrm{Q}) \Rightarrow(\mathrm{P} \wedge \mathrm{Q})$

Correct Option:

Solution:

$((P \rightarrow Q) \wedge \sim Q)$

$\equiv(\sim P \vee Q) \wedge \sim Q$

$\equiv(\sim P \wedge \sim Q) \vee(Q \wedge \sim Q)$

$\equiv \sim P \wedge \sim Q$

(A) $(P \wedge \sim Q) \rightarrow Q$

LHS of all the options are some i.e.

$\equiv \sim(\sim P \wedge \sim Q) \vee Q$

$\equiv(P \vee Q) \vee Q \neq$ tautology

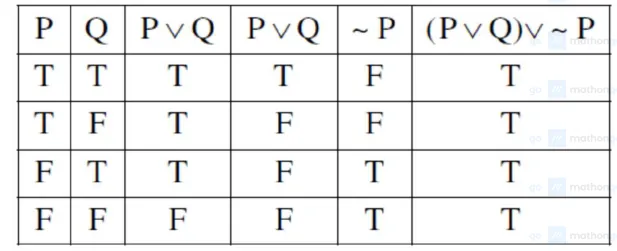
(B) $(\sim P \wedge \sim Q) \rightarrow \sim P$

$\equiv \sim(\sim P \wedge \sim Q) \vee \sim P$

$\equiv(P \vee Q) \vee \sim P$

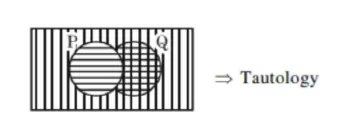
(C) $(\sim \mathrm{P} \wedge \sim \mathrm{Q}) \rightarrow \mathrm{P}$

$\equiv(P \vee Q) \vee P \neq$ Tautology

(D) $(\sim P \wedge \sim Q) \rightarrow(P \wedge Q)$

$\equiv(P \vee Q) \vee(P \wedge Q) \neq$ Tautology

Aliter:

 

Leave a comment

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material