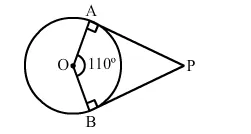
If PA and PB are two tangents to a circle with centre O, such that ∠AOB = 110°, find ∠APB.

(c) 70°

Given, $\mathrm{PA}$ and $\mathrm{PB}$ are tangents to a circle with centre $\mathrm{O}$, with $\angle \mathrm{AOB}=110^{\circ}$.

Now, we know that tangents drawn from an external point are perpendicular

to the radius at the point of contact.

So, $\angle \mathrm{OAP}=90^{\circ}$ and $\angle \mathrm{OBP}=90^{\circ}$.

$\Rightarrow \angle \mathrm{OAP}+\angle \mathrm{OBP}=90^{\circ}+90^{\circ}=180^{\circ}$, which shows that $\mathrm{OABP}$ is a cyclic

quadrilateral.

$\therefore \angle \mathrm{AOB}+\angle \mathrm{APB}=180^{\circ}$

$\Rightarrow 110^{\circ}+\angle \mathrm{APB}=180^{\circ}$

$\Rightarrow \angle \mathrm{APB}=180^{\circ}-110^{\circ}$

$\Rightarrow \angle \mathrm{APB}=70^{0}$