If $\sin \alpha$ and $\cos \alpha$ are the roots of the equations $a x^{2}+b x+c=0$, then $b^{2}=$
(a) $a^{2}-2 a c$
(b) $a^{2}+2 a c$
(c) $a^{2}-a c$
(d) $a^{2}+a c$
The given quadric equation is $a x^{2}+b x+c=0$, and $\sin \alpha$ and $\cos \beta$ are roots of given equation.
And, $a=a, b=b$ and, $c=c$
Then, as we know that sum of the roots
$\sin \alpha+\cos \beta=\frac{-b}{a} \ldots$(1)
And the product of the roots
$\sin \alpha \cdot \cos \beta=\frac{c}{a} \ldots$(2)
Squaring both sides of equation (1) we get
$(\sin \alpha+\cos \beta)^{2}=\left(\frac{-b}{a}\right)^{2}$
$\sin ^{2} \alpha+\cos ^{2} \beta+2 \sin \alpha \cos \beta=\frac{b^{2}}{a^{2}}$
Putting the value of $\sin ^{2} \alpha+\cos ^{2} \beta=1$, we get
$1+2 \sin \alpha \cos \beta=\frac{b^{2}}{a^{2}}$
$a^{2}(1+2 \sin \alpha \cos \beta)=b^{2}$
Putting the value of $\sin \alpha \cdot \cos \beta=\frac{c}{a}$, we get
$a^{2}\left(1+2 \frac{c}{a}\right)=b^{2}$
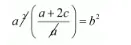
$a^{2}+2 a c=b^{2}$
Therefore, the value of $b^{2}=a^{2}+2 a c$
Thus, the correct answer is $(b)$
