If tangents are drawn to the ellipse

Given the equation of ellipse,

$\frac{x^{2}}{(\sqrt{2})^{2}}+y^{2}=1$

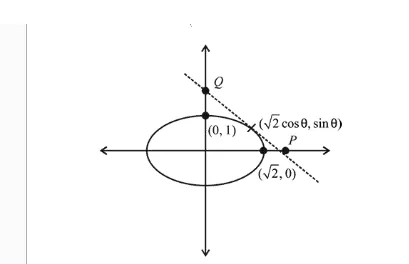
$\frac{\sqrt{2} \cos \theta x}{2}+y \sin \theta=1$

$P\left(\frac{\sqrt{2}}{\cos \theta}, 0\right)$ and $Q\left(0, \frac{1}{\sin \theta}\right)$

Let mid point be $(h, k)$

$\Rightarrow \quad h=\frac{1}{\sqrt{2} \cos \theta}, k=\frac{1}{2 \sin \theta}$

As $\cos ^{2} \theta+\sin ^{2} \theta=1$

$\therefore \quad \frac{1}{2 h^{2}}+\frac{1}{4 k^{2}}=1$]

Locus is $\frac{1}{2 x^{2}}+\frac{1}{4 y^{2}}=1$