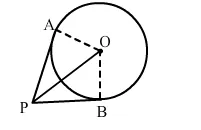
If tangents PA and PB from a point P to a circle with centre O

(b) 50°

From $\Delta O P A$ and $\Delta O P B$

$O A=O B(\mathrm{R}$ adi i of the same circle $)$

$O P(C$ ommon side $)$

$P A=P B$ (S ince tangents drawn from an external point to a circle are equal)

$\therefore \Delta O P A \cong \Delta O P B$ (SSS rule)

$\therefore \angle A P O=\angle B P O$

$\therefore \angle A P O=\frac{1}{2} \angle A P B=40^{\circ}$

$A$ nd $\angle O A P=90^{\circ}$ (S ince tangents drawn from an external point are

perpendicular to the radius at point of contact)

Now, in $\triangle O A P, \angle A O P+\angle O A P+\angle A P O=180^{\circ}$

$\Rightarrow \angle A O P+90^{\circ}+40^{\circ}=180^{\circ}$

$\Rightarrow \angle A O P=180^{0}-130^{0}=50^{0}$