If the angle between two tangents drawn from an external point

Let $\mathrm{PA}$ and $\mathrm{PB}$ be the two tangents drawn to the circle with centre $\mathrm{O}$ and radius a such that $\angle \mathrm{APB}=60^{\circ}$.

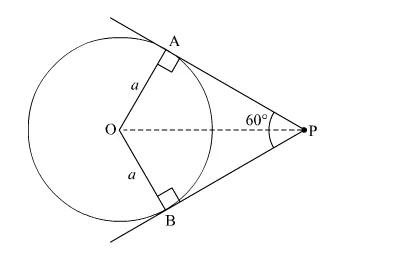
In ∆OPB and ∆OPA
OB = OA = a                    (Radii of the circle)

$\angle \mathrm{OBP}=\angle \mathrm{OAP}=90^{\circ} \quad$ (Tangents are perpendicular to radius at the point of contact)

BP = PA                            (Lengths of tangents drawn from an external point to the circle are equal)
So, ∆OPB ≌ ∆OPA           (SAS Congruence Axiom)  

$\therefore \angle \mathrm{OPB}=\angle \mathrm{OPA}=30^{\circ} \quad(\mathrm{CPCT})$

Now,
In ∆OPB,

$\sin 30^{\circ}=\frac{\mathrm{OB}}{\mathrm{OP}}$

$\Rightarrow \frac{1}{2}=\frac{a}{\mathrm{OP}}$

$\Rightarrow \mathrm{OP}=2 a$

Thus, the length of OP is 2a.
Disclaimer: The answer given in the book is incorrect.