If the area (in sq. units) bounded by the parabola

Given parabola $y^{2}=4 \lambda x$ and the line $y=\lambda x$

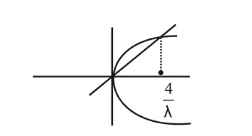
Putting $y=\lambda$ in $v^{2}=4 \lambda x$, we get $x=0.4$

$\therefore$ required area $=\int_{0}^{\frac{4}{\lambda}}(2 \sqrt{\lambda x}-\lambda x) d x$

$=\frac{2 \sqrt{\lambda} \cdot x^{3 / 2}}{3 / 2}-\left.\frac{\lambda x^{2}}{2}\right|_{0} ^{4 / \lambda}=\frac{32}{3 \lambda}-\frac{8}{\lambda}$

$=\frac{8}{3 \lambda}=\frac{1}{9} \Rightarrow \lambda=24$