If the area (in sq. units) of the region

Consider $y^{2}=4 x$ and $x+y=1$

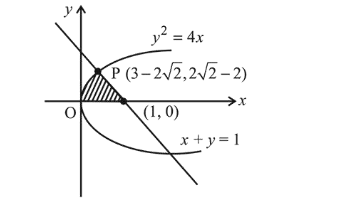
Substituting $x=1-y$ in the equation of parabola,

$y^{2}=4(1-y) \Rightarrow y^{2}+4 y-4=0$

$\Rightarrow(y+2)^{2}=8 \Rightarrow y+2=\pm 2 \sqrt{2}$

Hence, required area

$=\int_{0}^{3-2 \sqrt{2}} 2 \sqrt{x} d x+\frac{1}{2} \times(2 \sqrt{2}-2) \times(2 \sqrt{2}-2)$

$=\left[2 \times \frac{2}{3} x^{3 / 2}\right]_{0}^{3-2 \sqrt{2}}+\frac{1}{2}(8+4-8 \sqrt{2})$

$=\frac{4}{3} \times(3-2 \sqrt{2}) \sqrt{3-2 \sqrt{2}}+6-4 \sqrt{2}$

$=\frac{4}{3}(3-2 \sqrt{2})(\sqrt{2}-1)+6-4 \sqrt{2}$

$\left[\because(\sqrt{2}-1)^{2}=3-2 \sqrt{2}\right]$

$=\frac{4}{3}(3 \sqrt{2}-3-4+2 \sqrt{2})+6-4 \sqrt{2}$

$=-\frac{10}{2}+\frac{8}{3} \sqrt{2}=a \sqrt{2}+b$

$\therefore \quad a=8 / 3$ and $b=-10 / 3 \Rightarrow a-b=\frac{10}{3}+\frac{8}{3}=6$