If the list price of a toy is reduced by Rs. 2,

Solution:

Let the original list price of the toy be Rs. x .

Then, the number of toys brought for Rs. $360=\frac{360}{x}$

According to question, reduced list price of the toys $=$ Rs. $(x-2)$.

Therefore, the number of toys brought for Rs. $360=\frac{360}{x-2}$

It is given that

$\frac{360}{x-2}-\frac{360}{x}=2$

$\frac{360 x-360(x-2)}{(x-2) x}=2$

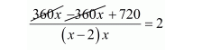
$\frac{720}{(x-2) x}=2$

$2\left(x^{2}-2 x\right)=720$

$\left(x^{2}-2 x\right)=360$

$x^{2}-2 x-360=0$

 

$x^{2}+18 x-20 x-360=0$

$x(x+18)-20(x+18)=0$

$(x+18)(x-20)=0$

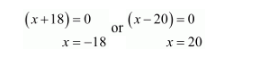
Because x cannot be negative.

Thus, $x=20$ is the require solution.

Therefore, the original list price of the toy be $x=$ Rs. 20