If the median of the following frequency distribution is 28.5 find the missing frequencies:

Given: Median = 28.5

We prepare the cumulative frequency table, as given below.

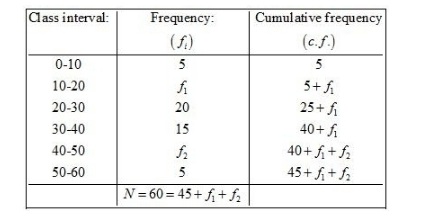
Now, we have

$N=60$

$45+f_{1}+f_{2}=60$

$f_{2}=15-f_{1}$.....(1)

$\mathrm{Also}, \frac{N}{2}=30$

Since the median $=28.5$ so the median class is $20-30$.

Here, $l=20, f=20, F=5+f_{1}$ and $h=10$

We know that

Median $=l+\left\{\frac{\frac{N}{2}-F}{f}\right\} \times h$

$28.5=20+\left\{\frac{30-\left(5+f_{1}\right)}{20}\right\} \times 10$

$8.5=\frac{\left(25-f_{1}\right) \times 10}{20}$

$8.5 \times 20=250-10 f_{1}$

$10 f_{1}=250-170$

$=80$

$f_{1}=8$

Putting the value of $f_{1}$ in (1), we get

$f=15-8$

$=7$

Hence, the missing frequencies are 7 and 8.