Question:
If the polynomial $\left(x^{4}+2 x^{3}+8 x^{2}+12 x+18\right)$ is divided by another polynomial $\left(x^{2}+5\right)$, the remainder comes out to be $(p x+q)$. Find the values of $p$ and $q$.
Solution:
Let $f(x)=x^{4}+2 x^{3}+8 x^{2}+12 x+18$
It is given that when $f(x)$ is divisible by $x^{2}+5$, the remainder comes out to be $p x+q$.
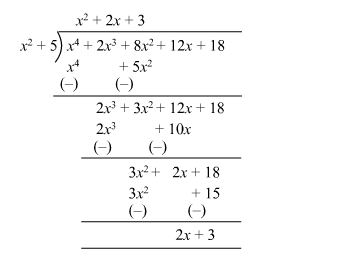
On division, we get the quotient $x^{2}+2 x+3$ and the remainder $2 x+3$
Since, the remainder comes out to be px + q.
Therefore, p = 2 and q = 3.
Hence, the values of p and q are 2 and 3 respectively.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.