If the quadratic equation 2x

For $2 x^{2}-\left(a^{3}+8 a-1\right) x+a^{2}-4 a=0$ has roots of opposite sign.

Let $\alpha$ and $\beta$ be 2 roots of above equation.

Then, according to give condition,

$\alpha \beta<0$

also, since sum of roots $=\frac{a^{3}+8 a-1}{2}$

$\Rightarrow \alpha+\beta=\frac{a^{3}+8 a-1}{2}$

and product of roots is $a^{2}-4 a$

i. e. $\alpha \beta=a^{2}-4 a$

since $\alpha \beta<0$

$\Rightarrow a^{2}-4 a<0$

i.e. $a(a-4)<0$

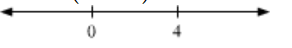
Since a(a – 4) < 0 is true for 0 < a < 4

Hence a ∈ (0, 4)