If the roots of the equation

For $x^{2}-8 x+a^{2}-6 a=0$

roots are real

Here $a=1, b=-8, c=a^{2}-6 a$

i.e. $D \geq 0$   (Discriminant)

i. e. $b^{2}-4 a c \geq 0$

i. e. $64-4(1)\left(a^{2}-6 a\right) \geq 0$

i.e. $64-4 a^{2}+24 a \geq 0$

i.e. $-4 a^{2}+24 a+64 \geq 0$

Now, multiplying by $-\frac{1}{4}$

i. e. $\frac{4 a^{2}}{4}-\frac{24 a}{4}-\frac{64}{4} \leq 0$

i. e. $a^{2}-6 a-16 \leq 0$

i. e. $a^{2}-8 a+2 a-16 \leq 0$

i.e. $a(a-8)+2(a-8) \leq 0$

i.e. $(a+2)(a-8) \leq 0$

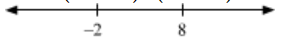
for $a<-2,(a+2)(a-8) \geq 0$ and for $a>8,(a+2)(a-8) \geq 0$