If the roots of the equation (c2−ab)x2−2(a2−bc)x+b2−ac=0 are equal,

The given quadric equation is $\left(c^{2}-a b\right) x^{2}-2\left(a^{2}-b c\right) x+\left(b^{2}-a c\right)=0$, and roots are equal.

Then prove that either $a=0$ or $a^{3}+b^{3}+c^{3}=3 a b c$

Here,

$a=\left(c^{2}-a b\right), b=-2\left(a^{2}-b c\right)$ and,$c=\left(b^{2}-a c\right)$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=\left(c^{2}-a b\right), b=-2\left(a^{2}-b c\right)$ and, $c=\left(b^{2}-a c\right)$

$D=b^{2}-4 a c$

$=\left\{-2\left(a^{2}-b c\right)\right\}^{2}-4 \times\left(c^{2}-a b\right) \times\left(b^{2}-a c\right)$

$=4\left(a^{4}-2 a^{2} b c+b^{2} c^{2}\right)-4\left(b^{2} c^{2}-a c^{3}-a b^{3}+a^{2} b c\right)$

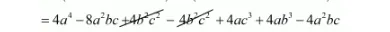
$=4 a^{4}-12 a^{2} b c+4 a c^{3}+4 a b^{3}$

$=4 a\left(a^{3}+b^{3}+c^{3}-3 a b c\right)$

The given equation will have real roots, if $D=0$

$4 a\left(a^{3}+b^{3}+c^{3}-3 a b c\right)=0$

$a\left(a^{3}+b^{3}+c^{3}-3 a b c\right)=0$

So, either

$a=0$

or

$\left(a^{3}+b^{3}+c^{3}-3 a b c\right)=0$

$a^{3}+b^{3}+c^{3}=3 a b c$

Hence $a=0$ or $a^{3}+b^{3}+c^{3}=3 a b c$