If the sides of a quadrilateral touch a circle. prove that the sum of a pair of opposite sides is equal to the sum of the other pair.
Let us first put the given data in the form of a diagram.
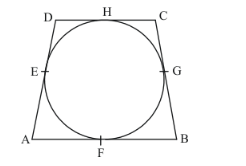
We have been asked to prove that the sum of the pair of opposite sides of the quadrilateral is equal to the sum of the other pair.
Therefore, we shall first consider,
AB + DC
But by looking at the figure we have,
AB + DC = AF + FB + DH + HC …… (1)
From the property of tangents we know that the length of two tangents drawn to a circle from a common external point will be equal. Therefore we have the following,
AF = AE
FB = BG
DH = ED
HC = CG
Replacing for all the above in equation (1), we have
AB + DC = AE + BG + ED + CG
AB + DC = (AE + ED) + (BG +CG)
AB + DC = AD + BC
Thus we have proved that the sum of the pair of opposite sides of the quadrilateral is equal to the sum of the other pair.
