If the sides of a triangle are produced in order, prove that the sum of the exterior angles so formed is equal to four right angles.
Question:
If the sides of a triangle are produced in order, prove that the sum of the exterior angles so formed is equal to four right angles.
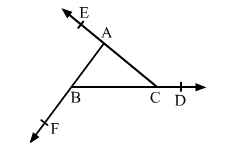
Solution:
Side BC of triangle ABC is produced to D.
$\angle A C D=\angle B+\angle A \ldots(i)$
Side AC of triangle ABC is produced to E.
$\angle B A C=\angle B+\angle C \quad \ldots(i)$
And side AB of triangle ABC is produced to F.
$\angle C B F=\angle C+\angle A \quad \ldots($ iii $)$
Adding $(i),(i i)$ and $(i i i)$, we get:
$\angle A C D+\angle B A E+\angle C B F=2(\angle A+\angle B+\angle C)$
$=2(180)^{\circ}$
$=360^{\circ}=4 \times 90^{\circ}=4$ right angle $s$
Hence, the sum of the exterior angles so formed is equal to four right angles.
