Question:
$f(x)=16 x^{2}-16 x+28$ on $R$
Solution:
Given: $f(x)=16 x^{2}-16 x+28$
$\Rightarrow f(x)=4\left(4 x^{2}-4 x+1\right)+24$
$\Rightarrow f(x)=4(2 x-1)^{2}+24$
Now,
$4(2 x-1)^{2} \geq 0$ for all $x \in R$
$\Rightarrow f(x)=4(2 x-1)^{2}+24 \geq 24$ for all $x \in R$
$\Rightarrow f(x) \geq 24$ for all $x \in R$
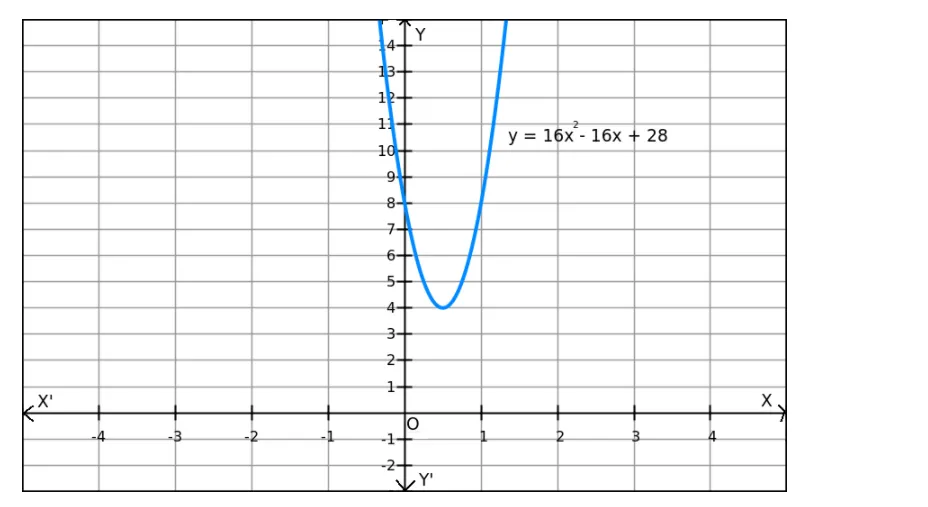
The minimum value of $f$ is attained when $(2 x-1)=0$.
$(2 x-1)=0$
$\Rightarrow x=\frac{1}{2}$
Therefore, the minimum value of $f$ at $x=\frac{1}{2}$ is 24 .
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
