Question:
$f(x)=|\sin 4 x+3|$ on $R$
Solution:
Given: $f(x)=|\sin 4 x+3|$
We know that $-1 \leq \sin 4 x \leq 1$.
$\Rightarrow 2 \leq \sin 4 x+3 \leq 4$
$\Rightarrow 2 \leq|\sin 4 x+3| \leq 4$
$\Rightarrow 2 \leq f(x) \leq 4$
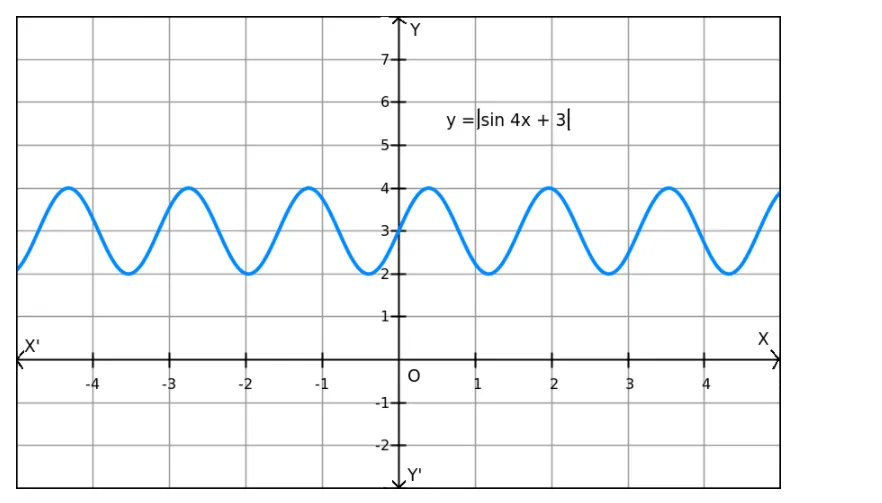
Hence, the maximum and minimum values of $f$ are 4 and 2 , respectively.
