Question:
$f(x)=\frac{1}{x^{2}+2}$
Solution:
Given : $f(x)=\frac{1}{x^{2}+2}$
$\Rightarrow f^{\prime}(x)=\frac{-2 x}{\left(x^{2}+2\right)^{2}}$
For the local maxima or minima, we must have
$f^{\prime}(x)=0$
$\Rightarrow \frac{-2 x}{\left(x^{2}+2\right)^{2}}=0$
$\Rightarrow x=0$
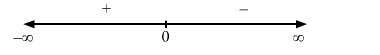
Now, for values close to $x=0$ and to the left of $0, f^{\prime}(x)>0$.
Also, for values close to $x=0$ and to the right of $0, f^{\prime}(x)<0$.
Therefore, by first derivative test, $x=0$ is a point of local maxima and the local maximum value of $f(x)$ is $\frac{1}{2}$.