If the sum of the roots of the equation x2−(k+6)x+2(2k−1)=0

Solution:

The given quadric equation is $x^{2}-(k+6) x+2(2 k-1)=0$, and roots are equal

Then find the value of k.

Let $\alpha$ and $\beta$ be two roots of given equation

And, $a=1, b=-(k+6)$ and,$c=2(2 k-1)$

Then, as we know that sum of the roots

$\alpha+\beta=\frac{-b}{a}$

$\alpha+\beta=\frac{-\{-(k+6)\}}{1}$

$=(k+6)$

And the product of the roots

$\alpha \cdot \beta=\frac{c}{a}$

$\alpha \beta=\frac{2(2 k-1)}{1}$

$=2(2 k-1)$

According to question, sum of the roots $=\frac{1}{2} \times$ product of the roots

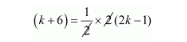
$k+6=2 k-1$

$6+1=2 k-k$

$7=k$

Therefore, the value of $k=7$

Thus, the correct answer is