If the tangent at a point P to a circle with centre O cuts a line through

Let us first draw whatever is given so that we can understand the problem better.

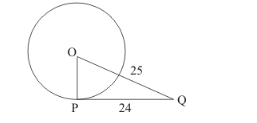
Since the tangent to a circle is always perpendicular to the radius of the circle at the point of contact, we have drawn OP perpendicular to PQ. Thus we have a right triangle with one of its sides as the radius. To find the radius we have to use Pythagoras theorem.

$O P^{2}=O Q^{2}-P Q^{2}$

$O P^{2}=25^{2}-24^{2}$

$O P^{2}=(25-24)(25+24)$

$O P^{2}=1 \times 49$

$O P^{2}=49$

$O P=\sqrt{49}$

$O P=7$

Therefore the radius of the circle is 7 cm.