If three circles of radius a each, are drawn such that each touches the other

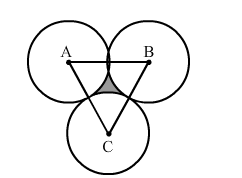
When three circles touch each other, their centres form an equilateral triangle, with each side being 2a.

Area of the triangle $=\frac{\sqrt{3}}{4} \times 2 a \times 2 a=\sqrt{3} a^{2}$

Total area of the three sectors of circles $=3 \times \frac{60}{360} \times \frac{22}{7} \times a^{2}=\frac{1}{2} \times \frac{22}{7} \times a^{2}=\frac{11}{7} a^{2}$

Area of the region between the circles = Area of the triangle - Area of the three sectors

$=\left(\sqrt{3}-\frac{11}{7}\right) a^{2}$

$=(1.73-1.57) a^{2}$

$=0.16 a^{2}$

$=\frac{4}{25} a^{2}$