If two adjacent vertices of a parallelogram are (3, 2) and (–1, 0) and the diagonals intersect at (2, –5)

Let ABCD be the parallelogram with two adjacent vertices A(3, 2) and B(−1, 0). Suppose O(2, −5) be the point of intersection of the diagonals AC and BD.
Let C(x1, y1) and D(x2, y2) be the coordinates of the other vertices of the parallelogram.

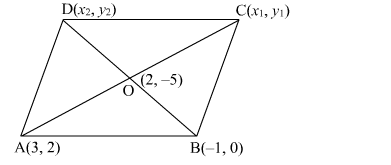
We know that the diagonals of the parallelogram bisect each other. Therefore, O is the mid-point of AC and BD.
Using the mid-point formula, we have

$\left(\frac{x_{1}+3}{2}, \frac{y_{1}+2}{2}\right)=(2,-5)$

$\Rightarrow \frac{x_{1}+3}{2}=2$ and $\frac{y_{1}+2}{2}=-5$

$\Rightarrow x_{1}+3=4$ and $y_{1}+2=-10$

$\Rightarrow x_{1}=4-3=1$ and $y_{1}=-10-2=-12$

So, the coordinates of C are (1, −12).
Also,

$\left(\frac{x_{2}+(-1)}{2}, \frac{y_{2}+0}{2}\right)=(2,-5)$

$\Rightarrow \frac{x_{2}-1}{2}=2$ and $\frac{y_{2}}{2}=-5$

$\Rightarrow x_{2}-1=4$ and $y_{2}=-10$

$\Rightarrow x_{2}=4+1=5$ and $y_{2}=-10$

So, the coordinates of D are (5, −10).