If two pipes function simultaneously, a reservoir will be filled in 12 hours.

Let the first pipe takes $x$ hours to fill the reservoir. Then the second pipe will takes $=(x+10)$ hours to fill the reservoir.

Since, the faster pipe takes $x$ hours to fill the reservoir.

Therefore, portion of the reservoir filled by the faster pipe in one hour $=\frac{1}{x}$

So, portion of the reservoir filled by the faster pipe in 12 hours $=\frac{12}{x}$

Similarly,

Portion of the reservoir filled by the slower pipe in 12 hours $=\frac{12}{x+10}$

It is given that the reservoir is filled in 12 hours.

So,

$\frac{12}{x}+\frac{12}{x+10}=1$

$\frac{12(x+10)+12 x}{x(x+10)}=1$

$12 x+120+12 x=x^{2}+10 x$

$x^{2}+10 x-24 x-120=0$

$x^{2}-14 x-120=0$

$x^{2}-20 x+6 x-120=0$

$x(x-20)+6(x-20)=0$

$(x-20)(x+6)=0$

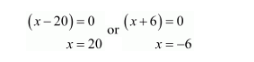
But, $x$ cannot be negative.

Therefore, when $x=20$ then

$(x+10)=20+10$

$=30$

Hence, the second pipe will takes 30 hours to fill the reservoir.