If two straight lines intersect in such a way that one of the angles formed measures 90°,

We know that if two lines intersect, then the vertically-opposite angles are equal.

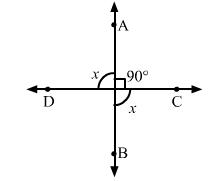
$\angle A O C=90^{\circ}$. Then, $\angle A O C=\angle B O D=90^{\circ}$

And let $\angle B O C=\angle A O D=x$

Also, we know that the sum of all angles around a point is $360^{\circ}$

$\therefore \angle A O C+\angle B O D+\angle A O D+\angle B O C=360^{\circ}$

$\Rightarrow 90^{\circ}+90^{\circ}+x+x=360^{\circ}$

$\Rightarrow 2 x=180^{\circ}$

$\Rightarrow x=90^{\circ}$

Hence, $\angle B O C=\angle A O D=90^{\circ}$

$\therefore \angle A O C=\angle B O D=\angle B O C=\angle A O D=90^{\circ}$

Hence, the measure of each of the remaining angles is $90^{\circ}$.